Methodik zur Quantifizierung von Sicherheitsspannen

Kevin Bielstein, Tobias Eckernkemper, Philipp Michels, Helge Müller, Lena Ullrich, Quantitative Methoden, CredaRate Solutions GmbH[^1]

I. Einführung

Gemäß Art. 179 1. (f) der Regulation (EU) No. 575/2013 (kurz CRR: Capital Regulation Requirements) müssen Kreditinstitute und Wertpapierfirmen^[2] für die Schätzwerte ihrer Risikoparameter eine Sicherheitsspanne (kurz MoC: Margin of Conservatism) berücksichtigen. Die Sicherheitsspanne soll in Relation zum erwarteten Schätzfehler stehen^[3] und das Ausmaß etwaiger Mängel (z. B. fehlende Daten) widerspiegeln. Mit der Richtlinie „Guidelines on PD estimation, LGD estimation and the treatment of defaulted exposures“ (EBA/GL/2017/16, kurz EBA-GL) veröffentlichte die Europäische Bankenaufsichtsbehörde (kurz EBA) Ende 2017 erstmals konkrete aufsichtsrechtliche Anforderungen zur Bestimmung der Sicherheitsspanne für die Risikoparameter PD (Probability of Default), LGD (Loss Given Default) und EL_BE (Expected Loss Best Estimate). Für die praktische Umsetzung der Sicherheitsspanne enthält die EBA-GL jedoch wesentliche Freiheitsgrade.

In diesem Beitrag wird für den Risikoparameter PD ein Framework vorgeschlagen, das die Lücke zwischen den aufsichtsrechtlichen Anforderungen und einer praktischen Umsetzung in Bezug auf die Bestimmung der Sicherheitsspanne schließen soll.

Die von der Aufsicht geforderte Einteilung der Schätzunsicherheit in die drei Kategorien A, B und C bildet den Ausgangspunkt. Die Kategorie C stellt dabei den allgemeinen Schätzfehler dar, welcher auf Basis klassischer Verfahren der Statistik, z. B. über Standardfehler oder Varianzen, bestimmt werden kann. Die Kategorie B bezieht sich auf Änderungen der Geschäftsstrategie und fällt entsprechend in den Bereich der Repräsentativität. Die Kategorie A beinhaltet Datenmängel und methodische Mängel, die ein individuelles Vorgehen bedingen und sich somit nicht pauschal in einen bestehenden Analysebereich einordnen lassen. Der Fokus dieses Beitrags besteht darin, für den Bereich der Kategorie A ein strukturiertes und nachvollziehbares Vorgehen zu entwickeln. Dieses Framework soll dabei eine konkrete Struktur vorgeben, die den gesamten Prozess zur Bildung einer Sicherheitsspanne der Kategorie A von der Auslegung der relevanten aufsichtsrechtlichen Passagen über eine Systematik zur Identifikation der relevanten Unsicherheiten bis hin zur finalen Quantifizierung umfasst. 

Dieser Beitrag ist dabei in zwei Teile gegliedert. Im ersten Teil erfolgte die Einführung in die Thematik der Sicherheitsspanne und die Darstellung eines Frameworks zur Identifikation relevanter Mängel und dem daraus resultierenden Bedarf von Sicherheitsspannen der Kategorie A. Für die Identifikation potentieller Mängel wurde eine Matrix zugrunde gelegt, deren Dimensionen sich aus den potentiellen Quellen zusätzlicher Unsicherheit aus der EBA-GL und den Qualitätsmerkmalen aus dem „ECB guide to internal models“ (01/10/2019, kurz EGIM) zusammensetzen. Aus den spezifischen Erfahrungen aus den (Weiter-)Entwicklungen und Validierungen von Ratingmodellen kann eine Identifikation aller potentiellen Mängel erfolgen. Nach Erstellung einer Longlist aller potentiellen Mängel werden diese über die Anwendung eines standardisierten Prüfungsprozesses dahingehend bewertet, ob ein relevanter Mangel vorliegt und die Erhebung einer Sicherheitsspanne erforderlich ist (vgl. Abbildung 1, Prozessschritte I und II). 

Darauf aufsetzend wird im vorliegenden zweiten Teil des Beitrags eine Methodik zur Quantifizierung von Sicherheitsspannen entwickelt, die individuell auf einzelne Mängel angewandt werden kann. Im letzten Schritt wird auf die Zusammenführung einzelner Sicherheitsspannen zu einer gesamten Sicherheitsspanne der Kategorie A eingegangen (vgl. Abbildung 1, Prozessschritte III und IV).  

Abbildung 1: Überblick Verfahren zur Quantifizierung einer Sicherheitsspanne der Kategorie A

Beide Teile des Beitrags werden dabei durch konkrete Fallbeispiele (Kästen mit Praxisbeispielen) unterstützt und können damit als anschaulicher generischer Leitfaden dienen, um entsprechende Sicherheitsspannen für (auf eigenen Daten oder auf Pooldaten basierende) Ratingmodelle zu entwickeln.^[4]

II. Quantifizierung der Sicherheitsspanne der Kategorie A 

1. Methodik zur Quantifizierung

In diesem Abschnitt wird eine Methodik zur Quantifizierung einer Sicherheitsspanne der Kategorie A dargestellt. Die Methodik basiert exemplarisch auf einem Scoremodell zur Prognose von Ausfallwahrscheinlichkeiten. Die Methodik ist bewusst allgemein gehalten, sodass sie in abgewandelter Form auch zur Modellierung von Mängeln bzgl. der Ausfallrate oder anderer Risikoparameter verwendet werden kann.

Logistische Regression als Beispiel für ein Scoremodell

Bezeichnet die Indikatorvariable y_i das Ausfallereignis (1: Ausfall; 0: kein Ausfall) des i-ten Kreditnehmers, xi = (x_i,1, ..., x_i,m)' einen Vektor mit m Regressoren und ε_i den logistisch verteilten Fehlerterm. Die Modellgleichung der logistischen Regression lautet dann^[5]:

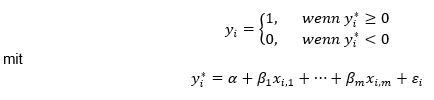
für i = 1, ..., N. Die prognostizierte Ausfallwahrscheinlichkeit (PD_i) und der Score (S_i) des i-ten Kreditnehmers ergeben sich dann zu: 

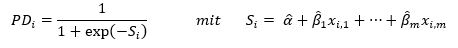
Ausgangspunkt zur Quantifizierung der Sicherheitsspanne ist die Kalibrierung der Ratingfunktion. Es wird angenommen, dass die Kalibrierung auf den langfristigen Durchschnitt der Ausfallrate (kurz LRADR: Long Run Average Default Rate) vorgenommen wurde^[6], sodass gilt:

mit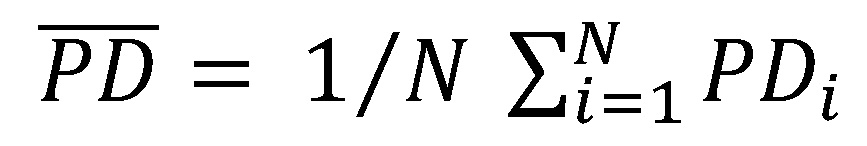, wobei PD_i der prognostizierten Ausfallwahrscheinlichkeit von Kreditnehmer i entspricht, und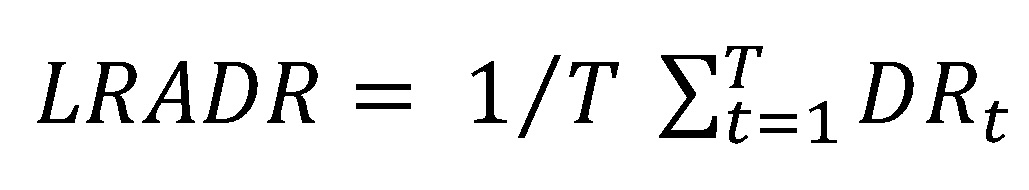, wobei DR_t der Ausfallrate (kurz Default Rate) der Zeitscheibe t (mit t = 1, ..., T) entspricht. Im Folgenden wird  als kalibrierungsrelevante PD-Prognose bezeichnet.

Jeder einzelne der identifizierten Mängel kann nun dazu führen, dass die Gleichung in Formel I nicht mehr erfüllt ist:

Dies ist der Fall, wenn die kalibrierungsrelevante PD-Prognose und/oder die LRADR ohne Mangel eigentlich kleiner oder größer wären als mit Mangel. In diesem Zusammenhang wird von einer Fehlkalibrierung gesprochen.^[7] 

Falls 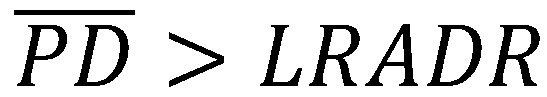handelt es sich um eine Überschätzung der langfristig durchschnittlichen Ausfallrate und bei  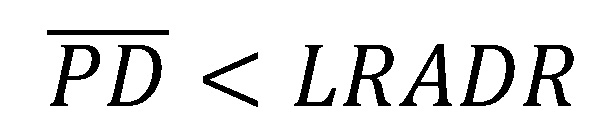um eine Unterschätzung der langfristig durchschnittlichen Ausfallrate. Bei der Überschätzung werden zu hohe Ausfallprognosen unterstellt, wohingegen bei der Unterschätzung zu geringe Ausfallprognosen unterstellt werden. In beiden Fällen handelt es sich somit um eine Verzerrung der Schätzung. Letzteres ist insbesondere problematisch für die Eigenkapitalhinterlegung, da diese möglicherweise zu gering ist.

In der EBA-GL wird die Art der Verzerrung allgemein gehalten. Im Folgenden wird jedoch die Überschätzung der Ausfallrate außer Acht gelassen, da von dieser kein generelles Risiko einer zu geringen Eigenmittelhinterlegung ausgeht. Das Risiko der möglichen Fehlkalibrierung bzw. Unterschätzung der Ausfallrate ist daher die Grundlage für das weitere Vorgehen und die Methodik zur Quantifizierung der Sicherheitsspanne der Kategorie A. 

Um das Niveau der Fehlkalibrierung je Mangel zu bestimmen, werden die Beobachtungen in zwei Gruppen aufteilt. Eine Gruppe beinhaltet die Beobachtungen mit Mangel und die andere Gruppe die Beobachtungen ohne Mangel. Die kalibrierungsrelevante PD-Prognose kann somit als gewichtetes arithmetisches Mittel aus dem Mittelwert der Gruppe mit und ohne Mangel (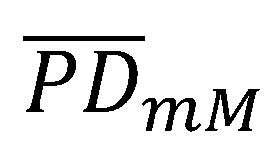und 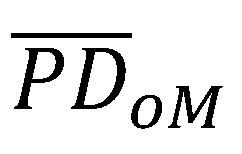) dargestellt werden:

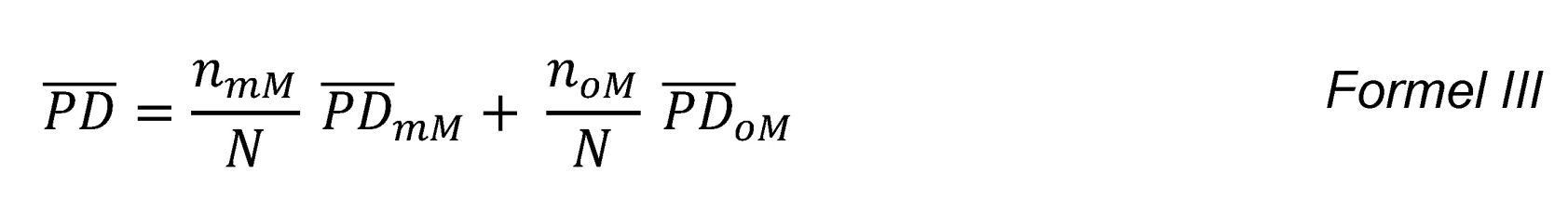
wobei 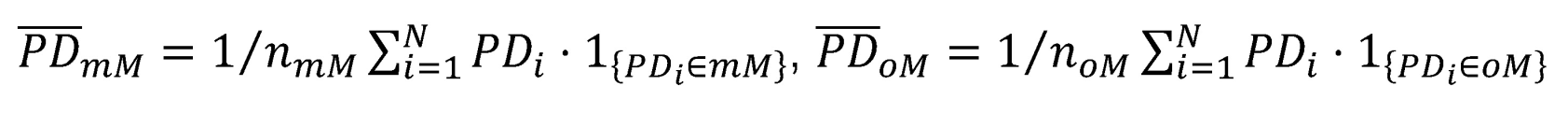und N = n_mM + n_oM. Die gewichtete Darstellung ermöglicht zum einen den direkten Vergleich der mittleren PD-Prognosen mit und ohne Mangel sowie zum anderen den Beitrag des betrachteten Mangels zum Gesamtniveau festzustellen. Beide Fälle ermöglichen, dass das Ausmaß des Mangels besser eingeschätzt werden kann.

Weiterhin wird angenommen, dass es neben einem zufälligen Fehler (vgl. z. B. die Modellgleichung der logistischen Regression) zusätzlich einen systematischen Fehler gibt. In Bezug auf die Gruppierung wird unterstellt, dass der systematische Fehler nur die Gruppe mit Mangel betrifft.

Für empirische Daten ist der funktionale Zusammenhang des systematischen Fehlers i. d. R. unbekannt. Zudem hängt der systematische Fehler stark vom jeweiligen Mangel ab, sodass dessen Quantifizierung häufig nicht möglich ist. Vor diesem Hintergrund werden modifizierte PD-Prognosen 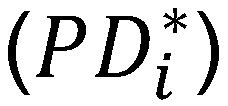 für die Gruppe mit Mangel ermittelt, welche die Verzerrung hinsichtlich des systematischen Fehlers bestmöglich widerspiegeln sollen und einen Proxy für das mögliche Ausmaß der Verzerrung darstellen. Auf Gesamtebene ergibt sich folglich ebenfalls eine modifizierte mittlere PD-Prognose:

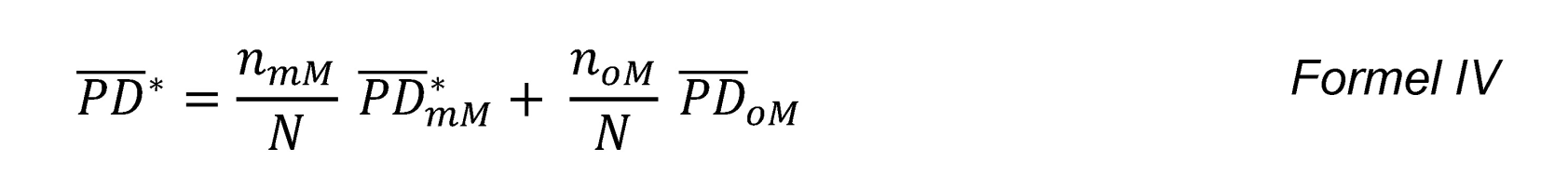
mit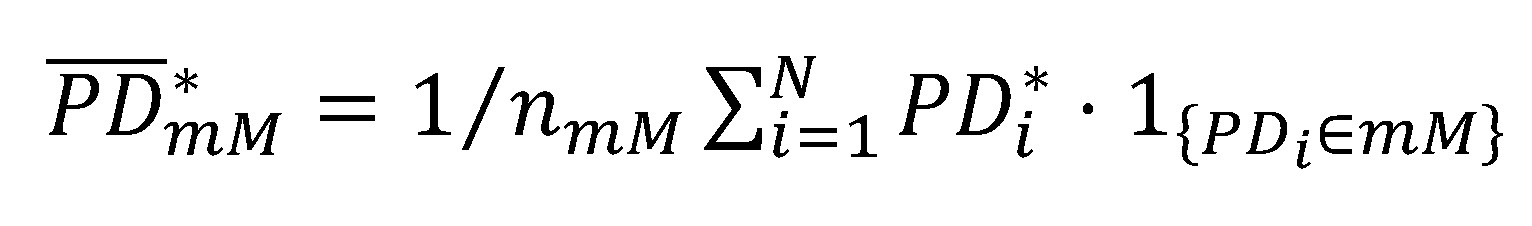. Die mittlere PD-Prognose der Gruppe mit Mangel ist daher der primäre Treiber für eine mögliche Verzerrung auf Gesamtebene. Neben der Höhe der PD-Prognosen bestimmt jedoch ebenfalls der Anteil der Beobachtungen mit Mangel maßgeblich die Höhe der mittleren modifizierten PD-Prognose, sodass – wenn nur wenige Kreditnehmer vom Mangel betroffen sind – das Gewicht  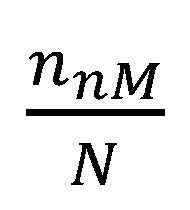klein ist und demnach die modifizierte mittlere PD-Prognose eine geringe Verzerrung aufweist.

Bestimmung der modifizierten PD-Prognose

Nachfolgend werden zwei Beispiele aufgeführt, wie die modifizierten PD-Prognosen bestimmt werden können.

Beispiel I: Im Zusammenhang mit allgemeinen Fehlern wird häufig ein additiver systematischer Fehler (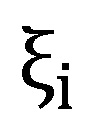) angenommen, sodass sich die modifizierte PD-Prognose wie folgt ergibt:

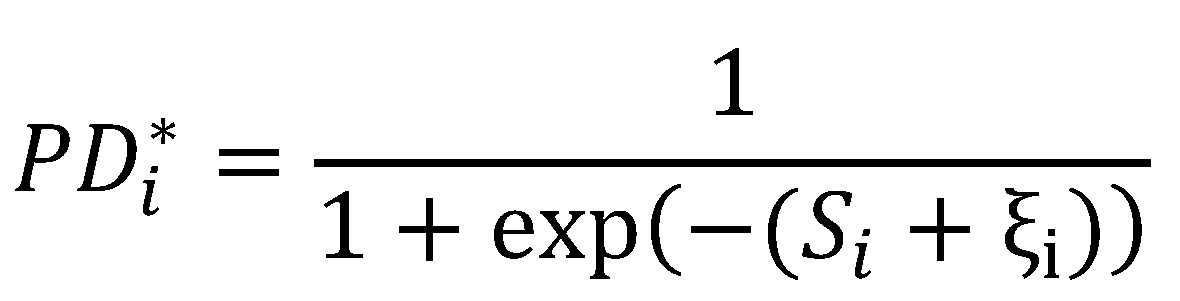
Die Wahl der Art des Fehlers sollte in Abhängigkeit des Mangels stattfinden. Dies betrifft vor allen Dingen die Struktur (dynamisch vs. konstant) und die Verteilung (parametrisch vs. nicht-parametrisch).

Beispiel II: Im Zusammenhang mit fehlenden Daten (vgl. EBA-GL Art. 37 a (v)) wird häufig ein parametrischer Simulationsalgorithmus zum Ersetzen der fehlenden Werte verwendet. In diesem Fall kann der Simulationsalgorithmus abermals für die betroffenen Beobachtungen angewandt werden, sodass sich ein alternativer Wert, z. B. 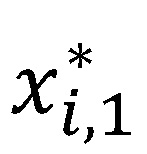 für den ersten Regressor, ergibt. Die modifizierte PD-Prognose ist dann:

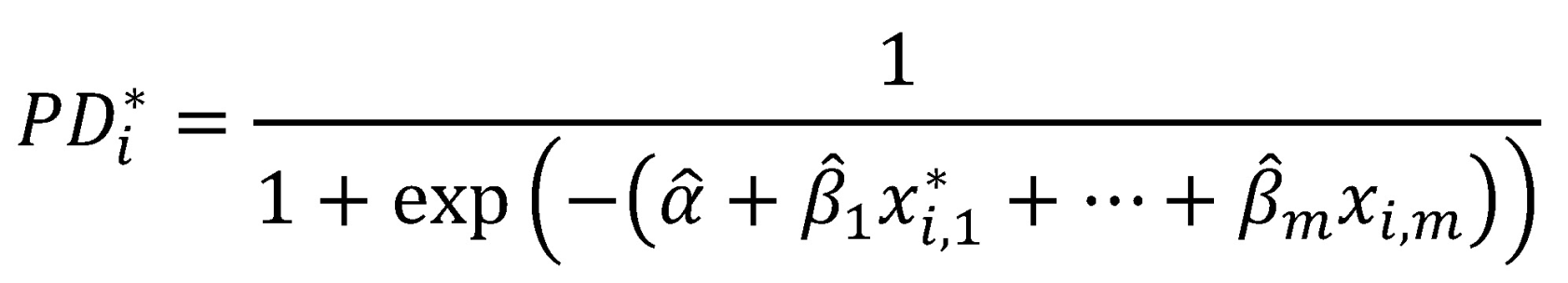
Die modifizierte PD-Prognose wird als Grundlage zur Quantifizierung der Sicherheitsspanne verwendet. Die Grundidee besteht darin, die Differenz zwischen der LRADR und einem (gestressten) Schätzwert basierend auf der Verteilung der modifizierten (mittleren) PD-Prognose zu bestimmen. 

Bestimmung der Verteilung

Die Verteilung kann mittels eines Bootstrap-Verfahrens bestimmt werden, indem bspw. aus der Gruppe mit Mangel eine einfache Stichprobe vom Umfang n_mM mit Zurücklegen gezogen wird. Auf Basis der Stichprobe kann die modifizierte PD-Prognose der Gruppe mit Mangel bestimmt und anschließend mit der mittleren PD-Prognose der Gruppe ohne Mangel gem. Formel IV zusammengeführt werden. Dieses Vorgehen wird S-mal wiederholt, sodass sich die Bootstrap-Stichprobe von modifizierten PD-Prognosen 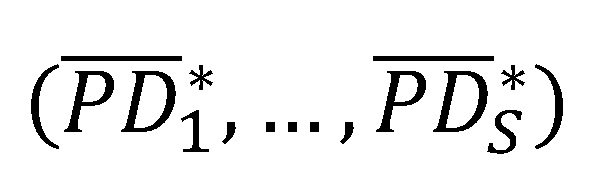ergibt. Diese kann als Grundlage zur Bestimmung entsprechender Verteilungscharakteristika verwendet werden.^[8]

Insbesondere vor dem Hintergrund, dass die Verzerrung eines Schätzers als Differenz zwischen dem wahren Wert und dem Erwartungswert des Schätzers abgebildet wird, ist die Bestimmung der Verteilung unabdingbar. Dieser Grundsatz wird zur Quantifizierung der Sicherheitspanne verwendet, sodass sich die Sicherheitspanne der Kategorie A und des Mangels j wie folgt ergibt:

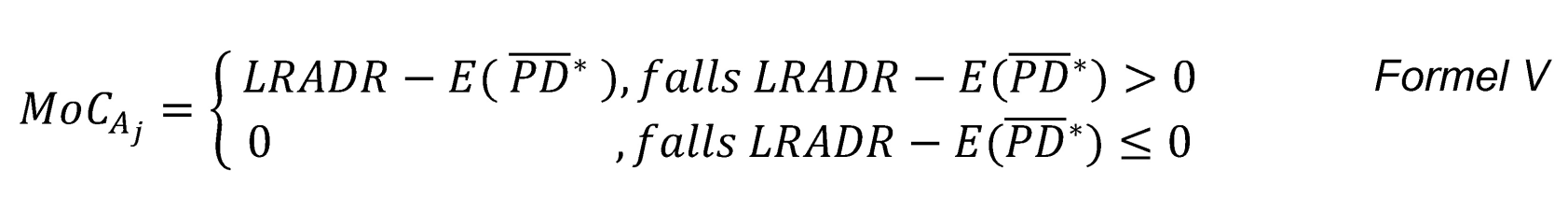
Da das Risiko in einer Unterschätzung der LRADR liegt (vgl. vorherige Darstellung), ist die Sicherheitsspanne bei nicht positiver Differenz gleich Null^[9] und ausschließlich für eine positive Differenz definiert. Das arithmetische Mittel der Bootstrap-Stichprobe dient hier als Schätzer des Erwartungswertes.

Alternativ zum Erwartungswert kann ein anderer Lageparameter verwendet werden, z. B. der Median oder ein beliebiges Quantil:

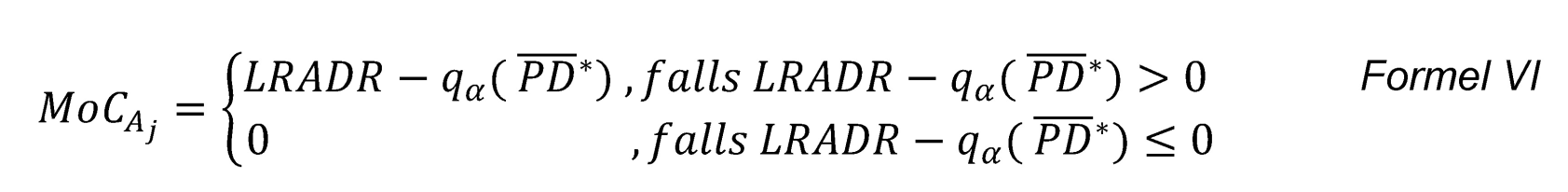
wobei 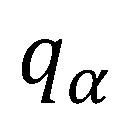dem 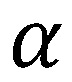-Quantil von 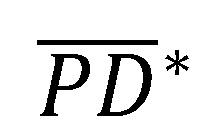entspricht. Das empirische 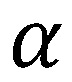-Quantil der Bootstrap-Stichprobe dient dann als Schätzer des 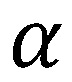-Quantils. In Abhängigkeit der Verteilung ist dieser Ansatz häufig weitaus konservativer als der Abstand der kalibrierungsrelevanten PD-Prognose zum Erwartungswert, da der Wert eines geeigneten Quantils i. d. R. links vom Erwartungswert liegt. Der Median würde bspw. einen Schätzer darstellen, der häufig in der Umgebung des Erwartungswerts liegt. Das 10%-Quantil hingegen würde einem stark gestressten Szenario am Rand der Verteilung entsprechen.

Beispiel zur Bestimmung einer Sicherheitsspanne^[10]

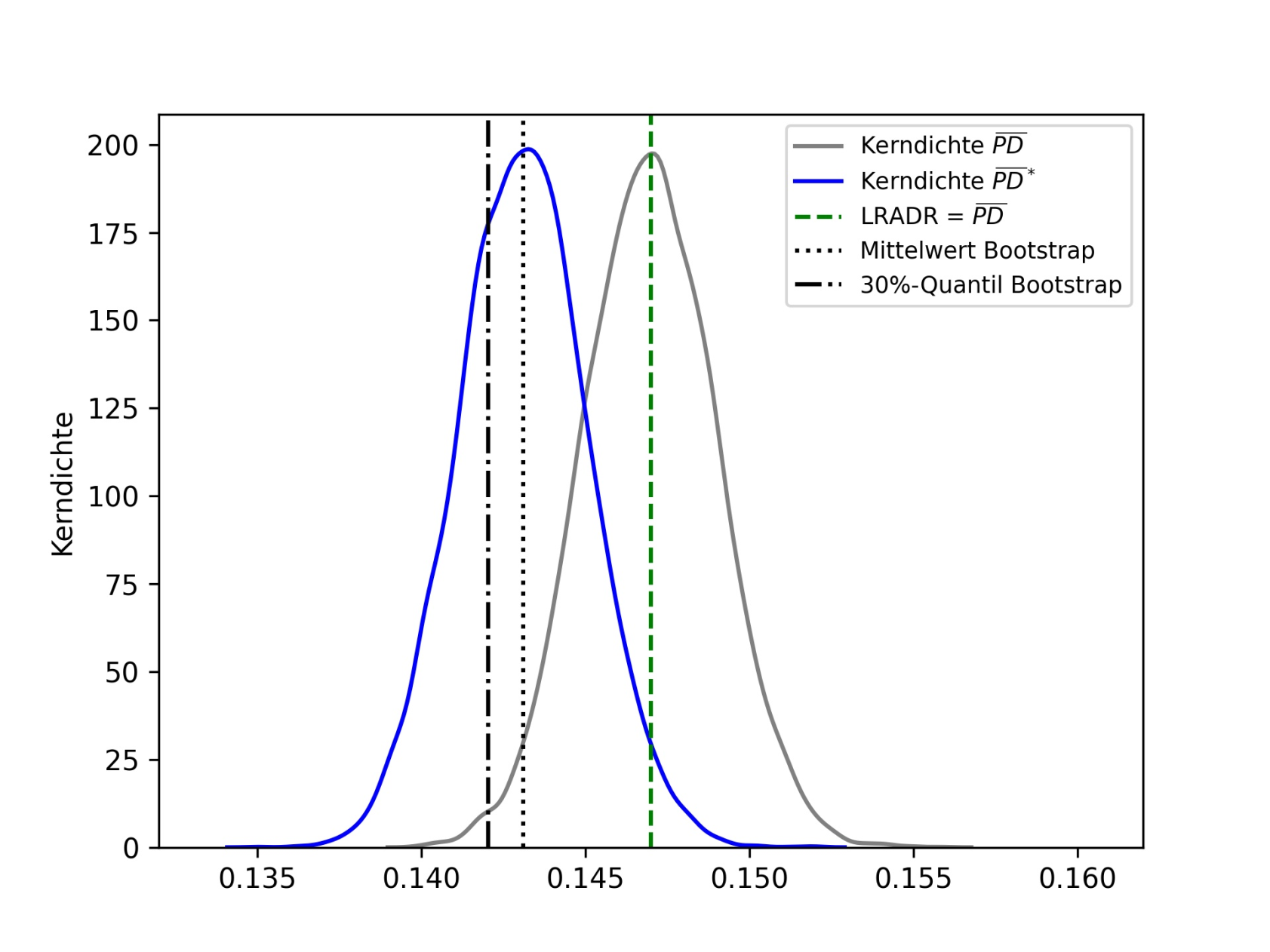
Angenommen der langfristige Durchschnitt der Ausfallrate sei LRADR = 0.147 und es wurde ein Logit-Modell für einen Datensatz (y_i, x_i)mit den Beobachtungen angepasst, sodass sich 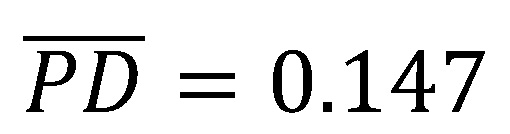als kalibrierungsrelevante PD-Prognose ergibt (vgl. Abb. 2: Verteilung mittlere PD-Prognosen, grün gestrichelte Linie).

Zudem sei bekannt, dass für die Hälfte der Beobachtungen eine Annahme getroffen wurde, die zwar den Best Estimate darstellt, aber mit Unsicherheit behaftet ist. Das zweitplausibelste Szenario für die Annahme verschiebt diese Ratings um einen konstanten Betrag und soll zur Erhebung einer Sicherheitsspanne genutzt werden. Mittels eines hinreichend konservativen Verfahrens wurde für die Gruppe mit Mangel, also die Hälfte der Beobachtungen, die modifizierte PD-Prognose bestimmt und die Verteilung auf Gesamtebene mittels des Bootstrap-Verfahrens ermittelt (vgl. Abb. 2: Verteilung mittlere PD-Prognosen, blaue Linie).

Auf Basis der Bootstrap-Stichprobe sei 0.1431 der Mittelwert der modifizierten PD-Prognosen (vgl. Abb.2: Verteilung mittlere, PD-Prognosen, gepunktete Linie) und 0.1420 das empirische – hier 30 % – Quantil (vgl. Abb. 2: Verteilung mittlere PD-Prognosen, gepunktete-gestrichelte Linie). Somit ergibt sich als Sicherheitsspanne:

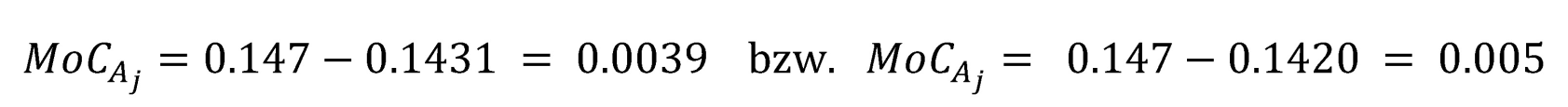
 Abbildung 2: Verteilung mittlere PD-Prognosen

Abschließend sei angemerkt, dass bei der Entwicklung einer Methodik zur Quantifizierung der Sicherheitsspanne immer ein Trade-off zwischen einem allgemein gültigen Verfahren und einem sehr speziellen Verfahren hinsichtlich der individuellen Charakteristika des jeweiligen Mangels besteht. Dieser Trade-off muss letztendlich individuell je Institut austariert werden.

2. Zusammenführung zur Sicherheitsspanne der Kategorie A

Die Zusammenführung zu einer gesamten Sicherheitsspanne der Kategorie A ist immer dann relevant, wenn mehr als ein Mangel innerhalb der jeweiligen Kategorie identifiziert wurde (z. B. .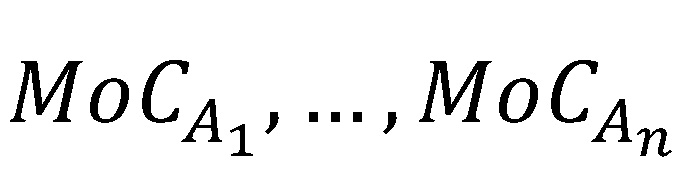

Im Gegensatz zur Zusammenführung auf oberster Ebene – für die explizit gefordert wird, dass die Sicherheitspannen der Kategorien A, B und C addiert werden sollen[11] – lässt die EBA-GL Freiraum bzgl. der Abhängigkeitsstruktur der Teilkategorien und somit der Zusammenführung. Insbesondere wird darauf verwiesen, dass Unabhängigkeit innerhalb der Kategorien durchaus eine mögliche Annahme sei.^[12]

Dementsprechend sollte die Zusammenführung innerhalb der Kategorien in Abhängigkeit der identifizierten Mängel und deren Zusammenhang durchgeführt werden. Stellen die identifizierten Mängel sehr unterschiedliche Sachverhalte dar, erscheint die Annahme der Unabhängigkeit durchaus plausibel^[13]. Falls die Mängel jedoch sehr eng miteinander verbunden sind und Überschneidungen aufweisen, erscheint die Unabhängigkeitsannahme weniger plausibel.

Zusammenführung innerhalb der Kategorien

Nachfolgend seien zwei Beispiele zur Zusammenführung gegeben.

Beispiel I: Analog zur Gesamtebene kann die Sicherheitspanne der Kategorie A als einfache Summe der Teilkategorien dargestellt werden:

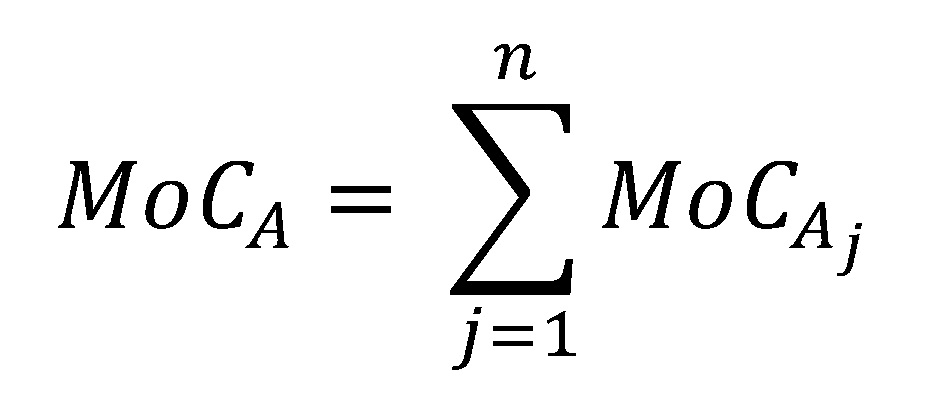
Dieser Ansatz ist relativ intuitiv und gewichtet jede Sicherheitspanne im gleichen Ausmaß. In Abhängigkeit der Anzahl und Höhe der Teilsicherheitsspannen kann durch einfaches Summieren die aggregierte Sicherheitsspanne allerdings relativ schnell unverhältnismäßig hoch werden, sodass das entsprechende Risiko nicht mehr adäquat abgebildet wird. In diesem Fall kann es durchaus sinnvoll sein, von der üblichen Zusammenführung abzuweichen, z. B. indem Verteilungsannahmen eingeführt werden.

Beispiel II: Unter der Annahme, dass die mittlere modifizierte PD-Prognose normalverteilt ist (bspw. mittels des Zentralen Grenzwertsatzes), stellen die Sicherheitsspannen der Teilkategorien – bei Verwendung des zuvor dargestellten Quantilansatzes – ebenfalls Quantile der Normalverteilung dar. Wird zusätzlich Unabhängigkeit zwischen den Mängeln der Teilkategorien angenommen, lässt sich das Quantil der Kategorie A als Wurzel der Summe der quadrierten Quantile der Teilkategorien darstellen:

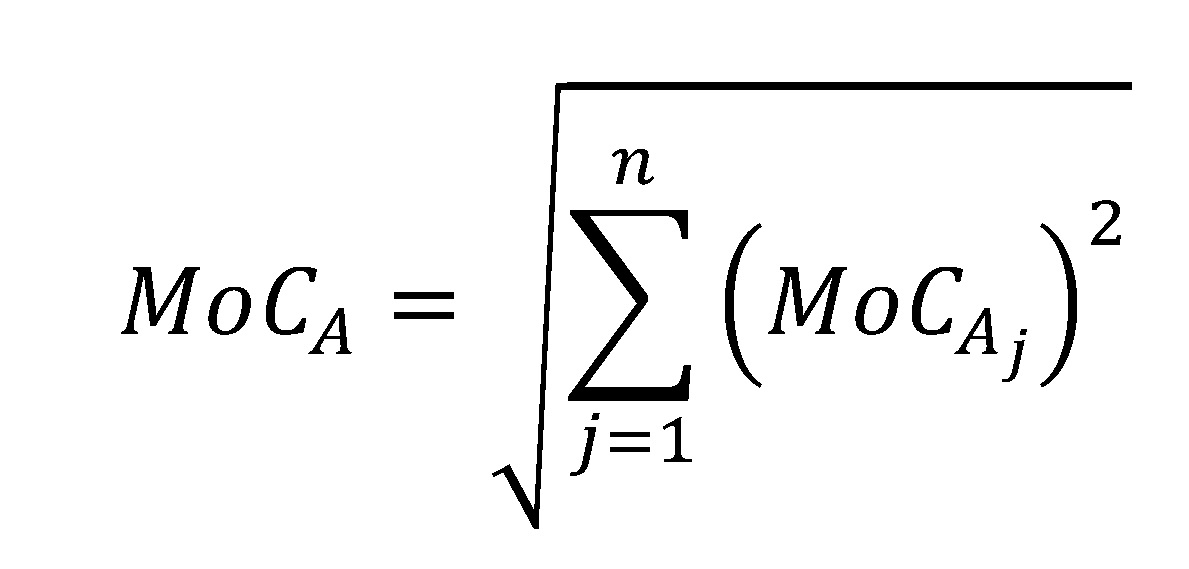
In Abhängigkeit der Ausprägung der Teilsicherheitsspannen, ergeben sich aufgrund der quadrierten Zusammenführung unterschiedliche Gewichtungen der einzelnen Mängel.^[14]

Angenommen es ergeben sich für zwei Sicherheitsspannen der Kategorie A folgende Werte:

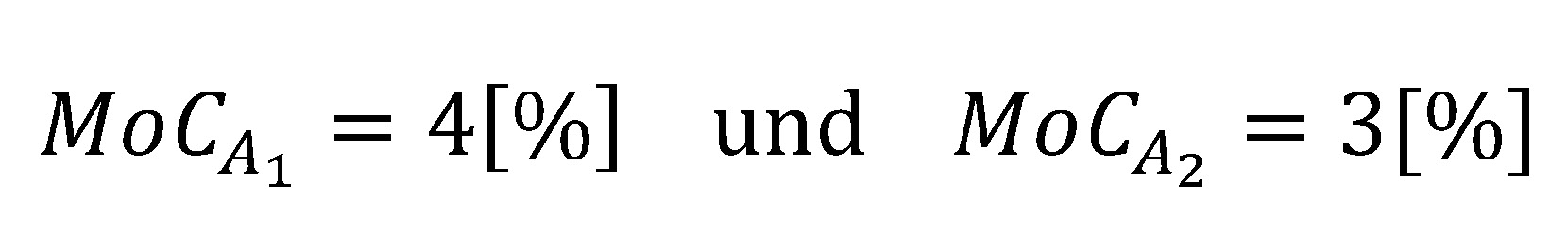
Damit ergäbe sich als Sicherheitsspanne der gesamten Kategorie A:

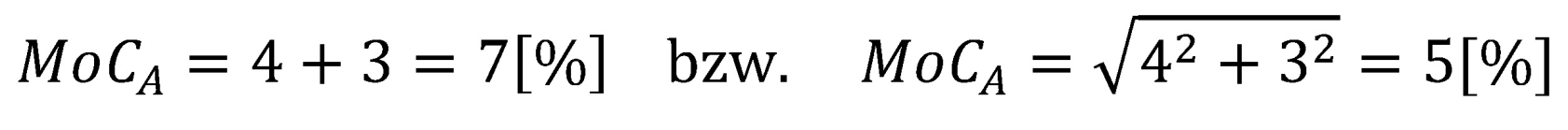
III. Zusammenfassung

Mit Veröffentlichung der EBA-Richtlinie „Guidelines on PD estimation, LGD estimation and the treatment of defaulted exposures“ wurden erstmals konkrete Anforderungen an die Bestimmung einer Sicherheitsspanne für die Schätzung von Risikoparametern gestellt. Bei der praktischen Umsetzung der Anforderungen bestehen jedoch erhebliche Freiheitsgrade. Daher wurde in diesem Beitrag für den Risikoparameter PD ein Framework entwickelt, das die praktische Umsetzung einer Sicherheitsspanne ermöglichen soll.

Ausgangspunkt ist die von der Aufsicht geforderte Einteilung der Unsicherheit der Schätzung in die drei Kategorien A, B und C. Die Kategorie C stellt den allgemeinen Schätzfehler dar und kann über Verfahren der klassischen Statistik ermittelt werden. Die Kategorie B bezieht sich auf die Änderungen der Geschäftsstrategie und fällt in den Bereich der Repräsentativität. Kategorie A beinhaltet Datenmängel und methodische Mängel, die ein individuelles Vorgehen benötigen und sich nicht pauschal einem Analysebereich zuordnen lassen. Der Fokus dieses Beitrags lag auf der Entwicklung eines strukturierten und nachvollziehbaren Vorgehens für diesen Bereich.

Das entwickelte Framework gibt dabei eine konkrete Struktur vor, die den gesamten Prozess zur Bildung einer Sicherheitsspanne der Kategorie A, von der Identifikation der relevanten Unsicherheiten bis zur finalen Quantifizierung, umfasst. 

Im ersten Teil des Beitrags wurde bereits ein Framework zur Identifikation der relevanten Mängel und dem daraus resultierenden Bedarf von Sicherheitsspannen vorgestellt. Im vorliegenden zweiten Teil des Beitrags wurde eine Methode zur Quantifizierung von Sicherheitsspannen entwickelt, die individuell auf die identifizierten Mängel angewandt werden kann. Das grundsätzliche Vorgehen besteht darin, modifizierte PD-Prognosen zu bestimmen, welche die Verzerrung hinsichtlich des systematischen Fehlers jedes Mangels bestmöglich widerspiegeln und somit einen Proxy für das mögliche Ausmaß der Verzerrung darstellen. Die Modellierung des Fehlers, z. B. in Bezug auf die Struktur (dynamisch vs. konstant) und die Verteilung (parametrisch vs. nicht-parametrisch), ist dabei vom betrachteten Mangel abhängig. Die Sicherheitsspanne kann schließlich als einfache Differenz zwischen der LRADR und dem gestressten Schätzwert auf Basis der modifizierten PD-Prognosen ermittelt werden.

Nachdem die Sicherheitsspannen für die einzelnen Mängel ermittelt wurden, ist die Zusammenführung zum gesamt MoC der Kategorie A vorzunehmen. Dabei wird vor allem auf die Abhängigkeitsstruktur zwischen den Mängeln eingegangen. Zuletzt kann die Zusammenführung des MoC A mit den Sicherheitsspannen der Kategorien B und C erfolgen. Diese ist konkret vom Aufsichtsrecht vorgegeben und erfolgt additiv. 

Das gesamte Framework deckt damit die wesentlichen Komponenten bei der Bestimmung der Sicherheitsspanne A ab und ermöglicht die Entwicklung individueller Konzepte zur Bestimmung der Sicherheitsspanne. Das Fundament bilden dabei allgemeine Konzepte, die ein breites Anwendungsgebiet und hohe Nachvollziehbarkeit ermöglichen. Gleichzeitig können individuelle Gegebenheiten abgebildet werden, wodurch sichergestellt wird, dass die gemessene Unsicherheit weitestgehend der tatsächlichen Unsicherheit entspricht.

PRAXISTIPPS 

• Als Ausgangspunkt für die Entwicklung einer Methodik zur Quantifizierung der Sicherheitsspanne sollte die Identifikation des Fehlkalibrierungs-Risikos (Unterschätzung der Ausfallrate) dienen.
• Der Trade-Off zwischen allgemeingültigen Verfahren für ein breites Anwendungsgebiet sowie hoher Transparenz und speziellen Verfahren zur Berücksichtigung individueller Gegebenheiten sollte austariert werden.
• Um die Verzerrung des systematischen Fehlers des jeweiligen Mangels bestmöglich abzubilden, sollten modifizierte PD-Prognosen für jeden Mangel verwendet werden.